Un intervalo real I, es la parte de los números reales que verifica la siguiente propiedad:
Si  y
y 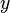 pertenecen a
pertenecen a  con
con 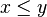 , entonces para todo
, entonces para todo  tal que
tal que  , se tiene que
, se tiene que  pertenece a I.
pertenece a I.
 y
y 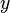 pertenecen a
pertenecen a  con
con 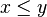 , entonces para todo
, entonces para todo  tal que
tal que  , se tiene que
, se tiene que  pertenece a I.
pertenece a I.
Los intervalos se determinan sobre la recta real y, por tanto, se corresponden con conjuntos de números. Pueden ser abiertos, cerrados o semiabiertos.

Intervalo Abierto
Un intervalo abierto de extremos a y b se designa (a, b) y representa al conjunto de los números reales comprendidos entre a y b, es decir, mayores que a pero menores que b: (a, b) = {x / a < x < b} Un intervalo semiabierto de extremos a y b puede ser (a, b] o [a, b):Intervalo Cerrado
Un intervalo cerrado es un segmento, AB, en el que se incluyen los extremos. Si las abscisas de los puntos A y B son respectivamente a y b, el intervalo cerrado se designa [a, b] y representa al conjunto de todos los números reales comprendidos entre a y b, incluyendo los extremos: [a, b] = {x / a ≤ x ≤ b}
Intervalo Semiabierto
Un intervalo semiabierto es un segmento AB en el que uno de los extremos es cerrado y el otro abierto.Un intervalo semiabierto de extremos a y b puede ser:
- (a, b] Intervalo abierto por la Izquierda y cerrado por la Derecha. Esta formado por todos los numeros mayores o iguales que a y menores o iguales a b.
(a, b] = {x / a < x ≤ b} (se excluye a y se incluye b)
- [a, b):Intervalo abierto por la Derecha y cerrado por la Izquierda. Está formado por todos los números que son mayores o iguales a a y menores que b.
[a, b) = {x / a ≤ x < b} (se incluye a y se excluye b)
Tipos De Intervalos

No hay comentarios.:
Publicar un comentario